.:: مجموعه عددهای طبیعی ::.

عددهای طبیعی: (natural nmuber)

طبیعی منسوب به طبیعت است و به معنی آنچه به طبیعت اختصاص دارد و مربوط به طبیعت است ، می باشد. هر یک از اعداد 1, 2 , 3, ... که در طبیعت برای شمارش از آن ها استفاده می شود را عدد طبیعی می نامیم. مجموعه عددهای طبیعی شامل اعداد طبیعی می باشد و آنرا با حرف که از کلمه انگلیسی Natural گرفته شده است، نمایش می دهند.

 {... , 3, 2, 1} =

عدد اول : (Prime Number)

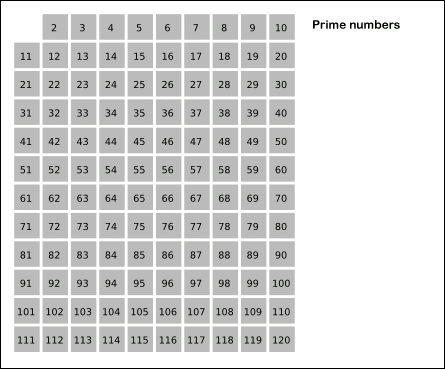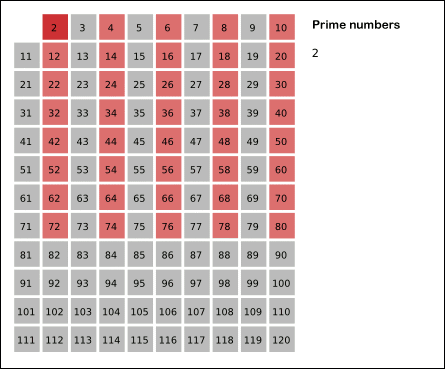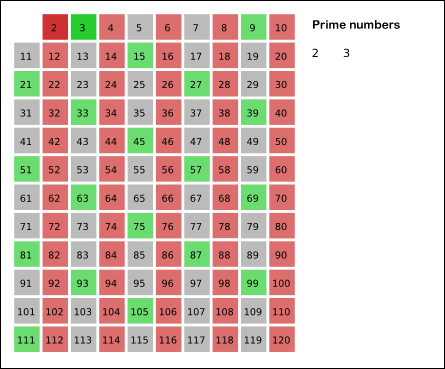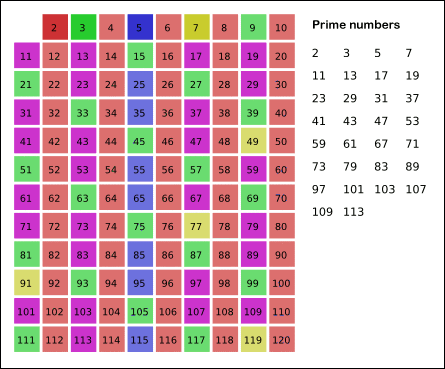
هر عدد طبیعی بزرگتر از یک که غیر از خودش و عدد یک مقسوم علیه دیگری نداشته باشد، عدد اول نامیده می شود. 2, 3, 5, 7 اعداد اول کوچکتر از 10 می باشند؛ هر عدد طبیعی که بیش از دو مقسوم علیه داشته باشد ، عدد مرکب نامیده می شود. 4, 6, 8, 9, اعداد مرکب کوچکتر از 10 هستند؛ عدد 1 نه اول است و نه مرکب.

تعیین عددهای اول:

برای مشخص کردن اعداد اول از بین عددهای طبیعی از الگوریتم غربال اراتستن استفاده می شود.

(sieve Algorithm of Eratosthenes)

اراتستن نام ریاضی دان و منجم یونانی است و غربال در فارسی به معنی جداکردن می باشد و الگوریتم به روشی از محاسبه گفته می شود که در آن ، محاسبات مرحله به مرحله انجام می شود و محاسبه هر مرحله نیز به مراحل قبلی بستگی دارد.

مراحل کار برای تعیین عددهای اول بین 1 و عدد طبیعی n به ترتیب نمودار زیر انجام می شود.

نويسنده : یاسین باژن | تاريخ : چهار شنبه 12 مهر 1391برچسب:,

| نوع مطلب : <-PostCategory-> |

.:: تشابه ::.

تشابه:(similarity )

تشابه به معنی به هم مانند بودن و به یکدیگر شبیه بودن می باشد. دو تصویر که از یک منظره تهیه شده اند ولی از لحاظ اندازه ها با هم تفاوت دارند, دو تصویر مشابهند.

پانتوگراف:(نقاله متحرک)

 نام وسیله ای است که برای رسم شکلهای متشابه از آن استفاده می شود.

نماد تشابه: برای نمایش تشابه دو شکل از نماد ~ استفاده می شود.

اگر شکل Aو'A متشابه باشند, می نویسیم:'A~A

در ادامه مطلب

ادامه مطلب ...
نويسنده : یاسین باژن | تاريخ : چهار شنبه 12 مهر 1391برچسب:,

| نوع مطلب : <-PostCategory-> |

.:: حجم ::.

حجم:(Volume)

حجم در لغت به معنی برآمدگی و ستبری و جسامت چیزی می باشد و در اصطلاح هندسه گنجایش و ظرفیت جسم و آن مقداری از فضا که جسم آن را اشغال می کند, را نشان می دهد.

منشور: (Prism)

منشور در لغت به معنی پراکنده, نشر شده, زنده شده و مبعوث است و در اصطلاح هندسه نام شکل است که دو قاعده دارد که دو چند ضلعی مساوی هستند و بدنه منشور(سطح جانبی منشور ) از مستطیلها یا متوازی الاضلاعها تشکیل شده است.

معرفی منشور 5 پهلو:

ي نام شکل: منشور 5 پهلو

ي یال های منشور: 'EE',DD',CC',BB',AA

ي وجه منشور: هر کدام از مستطیل های جانبی را یک وجه منشور می نامند.

ي ارتفاع منشور: از آنجا که هر کدام از یال ها بر دو قاعده منشور عمود می باشند, لذا ارتفاع منشور با اندازه هر یک از یال ها برابر است.

ي قاعده ی منشور: منشور دو قاعده دارد. ABCDE و 'A'B'C'D'E که دو پنج ضلعی مساوی اند.

رابطه های مهم:

ارتفاع × مساحت قاعده = حجم منشور

ارتفاع × محیط قاعده = مساحت جانبی منشور

مساحت دو قاعده + مساحت جانبی = مساحت کل منشور

استوانه: (Cylinder)

نام شکلی است که دو قاعده دارد که دو دایره مساوی هستند و بر جانبی راست استوار است.

اگر مستطیل را حول طول آن دوران دهیم, شکل فضایی حاصل استوانه نامیده می شود. در این صورت طول مستطیل ارتفاع استوانه و عرض آن شعاع قاعده استوانه می باشد.

 در شکل بالا مستطیل ABCD را حول طول آن دوران داده ایم و استوانه بوجود آمده است.

رابطه های مهم:

ارتفاع×مساحت قاعده(دایره) = حجم استوانه

ارتفاع×محیط قاعده(دایره) = مساحت جانبی استوانه

مساحت دو قاعده + مساحت جانبی = مساحت کل استوانه

در ادامه مطلب

ادامه مطلب ...
نويسنده : یاسین باژن | تاريخ : چهار شنبه 12 مهر 1391برچسب:,

| نوع مطلب : <-PostCategory-> |

مجموعه عددهای طبیعی 

عددهای طبیعی: (natural nmuber)

طبیعی منسوب به طبیعت است و به معنی آنچه به طبیعت اختصاص دارد و مربوط به طبیعت است ، می باشد. هر یک از اعداد 1, 2 , 3, ... که در طبیعت برای شمارش از آن ها استفاده می شود را عدد طبیعی می نامیم. مجموعه عددهای طبیعی شامل اعداد طبیعی می باشد و آنرا با حرف که از کلمه انگلیسی Natural گرفته شده است، نمایش می دهند.

 {... , 3, 2, 1} =

عدد اول : (Prime Number)

هر عدد طبیعی بزرگتر از یک که غیر از خودش و عدد یک مقسوم علیه دیگری نداشته باشد، عدد اول نامیده می شود. 2, 3, 5, 7 اعداد اول کوچکتر از 10 می باشند؛ هر عدد طبیعی که بیش از دو مقسوم علیه داشته باشد ، عدد مرکب نامیده می شود. 4, 6, 8, 9, اعداد مرکب کوچکتر از 10 هستند؛ عدد 1 نه اول است و نه مرکب.

تعیین عددهای اول:

برای مشخص کردن اعداد اول از بین عددهای طبیعی از الگوریتم غربال اراتستن استفاده می شود.

(sieve Algorithm of Eratosthenes)

اراتستن نام ریاضی دان و منجم یونانی است و غربال در فارسی به معنی جداکردن می باشد و الگوریتم به روشی از محاسبه گفته می شود که در آن ، محاسبات مرحله به مرحله انجام می شود و محاسبه هر مرحله نیز به مراحل قبلی بستگی دارد.

مراحل کار برای تعیین عددهای اول بین 1 و عدد طبیعی n به ترتیب نمودار زیر انجام می شود.

آزمون تشخیص اعداد اول:

برای بررسی اول بودن یک عدد ، ابتدا تمام اعداد اولی را که مربع آن ها کوچک تر یا مساوی عدد مورد نظر است، فهرست می کنیم. اگر عدد مورد نظر بر هیچکدام از آن ها بخشپذیر نباشد اول است؛ در غیر این صورت ، آن را    «عدد مرکب» می نامیم.

مثال: عدد 113 اول است یا مرکب؟

به عبارتی دیگر قاعده تشخیص اعداد اول را می توان این گونه بیان کرد:

عدد طبیعی n در صورتی اول است که بر هیچ کدام از اعداد اول کوچک تر یا مساوی بخشپذیر نباشد.

حل مسئله: در برخی از مسئله ها، تغییرات دو مقدار طوری است که حاصل ضرب آن ها ثابت می ماند. با مقایسه دو مقدار می توان فهمید که بین آن ارتباط معکوسی وجود دارد یعنی با زیاد شدن مقدار یکی، مقدار دیگری کاهش می یابد و برعکس. با تشخیص این موضوع و توجه به آن می توانیم این گونه مسئله ها را حل کنیم.

مثال: برای نقاشی یک ساختمان 3 کارگر 18 روز کار کردند. اگر می خواستند کار زودتر انجام شود، تعداد کارگران را باید بیشتر می کردند یا کمتر؟ اگر تعداد کارگر ها 6 نفر بود، این کار چند روزه انجام می شد؟

حل: تعداد کارگران باید بیشتر شود تا کار زودتر انجام گیرد.

می دانیم 3 کارگر 18 روز کار کرده اند ، حالا اگر تعداد کارگرها 6 نفر شود می توانیم رابطه زیر را در مورد این دو مقدار بنویسیم:   

و سپس انرا از راه معادله حل کنیم:

بنابراین: 6 کارگر 9 روزه کار را تمام خواهند کرد.

در این مسئله با افزوده شدن کارگران ،  زمان کار کم می شود، یعنی حاصل ضرب تعداد کارگران با زمان همواره مقداری ثابت است.

توان:

معادله توانی: معادله توانی معادله ای است که که در آن مجهول به صورت توان ظاهر شده است. مانند:  2^x=۸. برای حل چنین معادله هایی در صورت امکان دو طرف معادله را به دو عدد تواندار با پایه های مساوی تبدیل می کنیم ؛ آنگاه توانهای دو طرف را با هم مساوی قرار می دهیم و جواب معادله را بدست می آوریم.

مثال: معادله های توانی زیر را حل کنید.

حل: دو طرف تساوی بالا فقط در صورتی می توانند با هم مساوی باشند ، که توان عدد  7 برابر صفر باشد. بنابراین می توان نوشت:

1. هر عدد طبیعی بزرگتر از یک لااقل یک مقسوم علیه اول دارد.

2. اگر n عدد طبیی باشد ، داریم:

مثال: عدد ⁸ 10×5 چند رقمی است؟

حل: 9 رقمی است. زیرا:

3.

4. برای تجزیه یک عدد به عامل های اول، لازم است چند عدد اول از مجموعه اعداد اول را به خاطر سپرده و عدد را به ترتیب بر آنها تقسیم کنیم تا باقیمانده صفر شود.

مثال:

5. هر عدد منفی به توان عددی زوج برسد ، حاصل عددی مثبت است و اگر عدد منفی به توان عددی فرد برسد، حاصل عدد منفی خواهد بود.

6. اگر مجموع یا تفاضل دو عدد اول ، عددی فرد باشد ، حتما یکی از آن دو عدد 2 است.

7. در هر تناسب حاصل ضرب طرفین با حاصل ضرب وسطین مساوی است:

8. در تناسب  هر نوع تغییر در آرایش صورت و مخرج نسبتها به شرطی که تساوی ad=bc برقرار باشد، مجاز می باشد.

مثال:

نويسنده : یاسین باژن | تاريخ : چهار شنبه 12 مهر 1391برچسب:جزوه,

| نوع مطلب : <-PostCategory-> |